The figure below shows the numeric equivalents in binary, octal, and decimal of the first 16 hexadecimal numbers. If octal numbers were included, they would run from 00 through 017.

Binary Decimal Hexadecimal
(base 2) (base 10) (base 16)

0000 00 0

0001 01 1 Note that conversions from hexadecimal

0010 02 2 to binary can be done one digit at a time,

0011 03 3 thus DE = 11011110, as D = 1101 and

0100 04 4 E = 1110. We shall normally denote

0101 05 5 this as DE = 1101 1110 with a space

0110 06 6 to facilitate reading the binary.

0111 07 7

1000 08 8 Conversion from binary to hexadecimal

1001 09 9 is also quite easy. Group the bits four at

1010 10 A a time and convert each set of four.

1011 11 B Thus 10111101, written 1011 1101 for

1100 12 C clarity is BD because 1011 = B and

1101 13 D 1101 = D.

1110 14 E

1111 15 F

Consider conversion of the binary number 111010 to hexadecimal. If we try to group the bits four at a time we get either 11 1010 or 1110 10. The first option is correct as the grouping must be done from the right. We then add leading zeroes to get groups of four binary bits, thus obtaining 0011 1010, which is converted to 3A as 0011 = 3 and 1010 = A.

Conversions between Decimal and Binary

We now consider methods for conversion from decimal to binary and binary to decimal. We consider not only whole numbers (integers), but numbers with decimal fractions. To convert such a number, one must convert the integer and fractional parts separately.

Consider the conversion of the number 23.375. The method used to convert the integer part (23) is different from the method used to convert the fractional part (.375). We shall discuss two distinct methods for conversion of each part and leave the student to choose his/her favorite. After this discussion we note some puzzling facts about exact representation of decimal fractions in binary; e.g. the fact that 0.20 in decimal cannot be exactly represented in binary. As before we present two proofs and let the student choose his/her favorite and ignore the other.

The intuitive way to convert decimal 23 to binary is to note that 23 = 16 + 7 = 16 + 4 + 2 + 1. Thus decimal 23 = 10111 binary. As an eight bit binary number this is 0001 0111. Note that we needed 5 bits to represent the number; this reflects the fact that 2⁴ < 23 £ 2⁵. We expand this to an 8-bit representation by adding three leading zeroes.

The intuitive way to convert decimal 0.375 to binary is to note that 0.375 = 1/4 + 1/8 =
0/2 + 1/4 + 1/8, so decimal .375 = binary .011 and decimal 23.375 = binary 10111.011.

Most students prefer a more mechanical way to do the conversions. Here we present that method and encourage the students to learn this method in preference to the previous.

Conversion of integers from decimal to binary is done by repeated integer division with keeping of the integer quotient and noting the integer remainder. The remainder numbers are then read top to bottom as least significant bit to most significant bit. Here is an example.

Quotient Remainder

23/2 = 11 1 Thus decimal 23 = binary 10111

11/2 = 5 1

5/2 = 2 1 Remember to read the binary number

2/2 = 1 0 from bottom to top.

1/2 = 0 1

Conversion of the fractional part is done by repeated multiplication with copying of the whole number part of the product and subsequent multiplication of the fractional part. All multiplications are by 2. Here is an example.

Number Product Binary

0.375 x 2 = 0.75 0

0.75 x 2 = 1.5 1

0.5 x 2 = 1.0 1

The process terminates when the product of the last multiplication is 1.0. At this point we copy the last 1 generated and have the result; thus decimal 0.375 = 0.011 binary.

We now develop a “power of 2” notation that will be required when we study the IEEE floating point standard. We have just shown that decimal 23.375 = 10111.011 binary. Recall that in the scientific “power of 10” notation, when we move the decimal to the left one place we have to multiply by 10. Thus, 1234 = 123.4 · 10¹ = 12.34 · 10² = 1.234 · 10³.

We apply the same logic to the binary number. In the IEEE standard we need to form the number as a normalized number, which is of the form 1.xxx · 2^p. In changing 10111 to
1.0111 we have moved the decimal point (O.K. – it should be called binary point) 4 places to the left, so 10111.011 = 1.0111011 · 2⁴. Recalling that 2⁴ = 16 and 2⁵ = 32, and noting that 16.0 < 23.375 £ 32.0 we see that the result is as expected.

Conversion from binary to decimal is quite easy. One just remembers the decimal representations of the powers of 2. We convert 10111.011 binary to decimal. Recalling the positional notation used in all number systems:

10111.011 = 1·2⁴ + 0·2³ + 1·2² + 1·2¹ + 1·2⁰ + 0·2^-1 + 1·2^-2 + 1·2^-3

= 1·16 + 0·8 + 1·4 + 1·2 + 1·1 + 0·0.5 + 1·0.25 + 1·0.125
= 23.375

Conversions between Decimal and Hexadecimal

The conversion is best done by first converting to binary. We consider conversion of 23.375 from decimal to hexadecimal. We have noted that the value is 10111.011 in binary.

To convert this binary number to hexadecimal we must group the binary bits in groups of four, adding leading and trailing zeroes as necessary. We introduce spaces in the numbers in order to show what is being done.

10111.011 = 1 0111.011.

To the left of the decimal we group from the right and to the right of the decimal we group from the left. Thus 1.011101 would be grouped as 1.0111 01.

At this point we must add extra zeroes to form four bit groups. So

10111.011 = 0001 0111.0110.

Conversion to hexadecimal is done four bits at a time. The answer is 17.6 hexadecimal.

Non-terminating Fractions

We now make a detour to note a surprising fact about binary numbers – that some fractions that terminate in decimal are non-terminating in binary. We first consider terminating and non-terminating fractions in decimal. All of us know that 1/4 = 0.25, which is a terminating fraction, but that 1/3 = 0.333333333333333333333333333333…, a non-terminating fraction.

We offer a demonstration of why 1/4 terminates in decimal notation and 1/3 does not, and then we show two proofs that 1/3 cannot be a terminating fraction.

Consider the following sequence of multiplications

1/4 · 10 = 2½

½ · 10 = 5. Thus 1/4 = 25/100 = 0.25.

However, 1/3 · 10 = 10/3 = 3 + 1/3, so repeated multiplication by 10 continues to yield a fraction of 1/3 in the product; hence, the decimal representation of 1/3 is non-terminating.

In decimal numbering, a fraction is terminating if and only if it can be represented in the form J / 10^K for some integers J and K. We have seen that 1/4 = 25/100 = 25/10², thus the fraction 1/4 is a terminating fraction because we have shown the integers J = 25 and K = 2.

Here are two proofs that the fraction 1/3 cannot be represented as a terminating fraction in decimal notation. The first proof relies on the fact that every positive power of 10 can be written as 9·M + 1 for some integer M. The second relies on the fact that 10 = 2·5, so that 10^K = 2^K·5^K. To motivate the first proof, note that 10⁰ = 1 = 9·0 + 1, 10 = 9·1 + 1,

100 = 9·11 + 1, 1000 = 9·111 + 1, etc. If 1/3 were a terminating decimal, we could solve the following equations for integers J and M.

, which becomes 3·J = 9·M + 1 or 3·(J – 3·M) = 1. But there is no integer X such that 3·X = 1 and the equation has no integer solutions.

The other proof also involves solving an equation. If 1/3 were a non-terminating fraction, then we could solve the following equation for J and K.

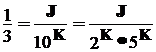, which becomes 3·J = 2^K·5^K. This has an integer solution J only if the right hand side of the equation can be factored by 3. But neither 2^K nor 5^K can be factored by 3, so the right hand side cannot be factored by 3 and hence the equation is not solvable.

Now consider the innocent looking decimal 0.20. We show that this does not have a terminating form in binary. We first demonstrate this by trying to apply the multiplication method to obtain the binary representation.

Number Product Binary

0.20 · 2 = 0.40 0
0.40 · 2 = 0.80 0

0.80 · 2 = 1.60 1

0.60 · 2 = 1.20 1

0.20 · 2 = 0.40 0

0.40 · 2 = 0.80 0

0.80 · 2 = 1.60 1 but we have seen this – see four lines above.

So decimal 0.20 in binary is 0.00110011001100110011 … ad infinitum.

The proof that no terminating representation exists depends on the fact that any terminating fraction in binary can be represented in the form for some integers J and K. Thus we solve or 5·J = 2^K. This equation has a solution only if the right hand side is divisible by 5. But 2 and 5 are relatively prime numbers, so 5 does not divide any power of 2 and the equation has no integer solution. Hence 0.20 in decimal has no terminating form in binary.

Binary Addition

The next topic is storage of integers in a computer. We shall be concerned with storage of both positive and negative integers. Two’s complement arithmetic is the most common method of storing signed integers. Calculation of the two’s complement of a number involves binary addition. For that reason, we first discuss binary addition.

To motivate our discussion of binary addition, let us first look at decimal addition. Consider the sum 15 + 17 = 32. First, note that 5 + 7 = 12. In order to speak of binary addition, we must revert to a more basic way to describe 5 + 7; we say that the sum is 2 with a carry-out of 1. Consider the sum 1 + 1, which is known to be 2. However, the correct answer to our simple problem is 32, not 22, because in computing the sum 1 + 1 we must consider the carry-in digit, here a 1. With that in mind, we show two addition tables – for a half-adder and a full-adder. The half-adder table is simpler as it does not involve a carry-in. The following table considers the sum and carry from A + B.

Half-Adder A + B

A B Sum Carry

0 0 0 0 Note the last row where we claim that 1 + 1 yields a

0 1 1 0 sum of zero and a carry of 1. This is similar to the

1 0 1 0 statement in decimal arithmetic that 5 + 5 yields a

1 1 0 1 sum of 0 and carry of 1 when 5 + 5 = 10.

Remember that when the sum of two numbers equals or exceeds the value of the base of the numbering system (here 2) that we decrease the sum by the value of the base and generate a carry. Here the base of the number system is 2 (decimal), which is 1 + 1, and the sum is 0.

For us the half-adder is only a step in the understanding of a full-adder, which implements binary addition when a carry-in is allowed. We now view the table for the sum A + B, with a carry-in denoted by C. One can consider this A + B + C, if that helps.

Full-Adder: A + B with Carry

A B C Sum Carry

0 0 0 0 0

0 0 1 1 0

0 1 0 1 0

0 1 1 0 1

1 0 0 1 0

1 0 1 0 1

1 1 0 0 1

1 1 1 1 1

Immediately, we have the Boolean implementation of a Full Adder; how to make such a

circuit using only AND, OR, and NOT gates.

As an example, we shall consider a number of examples of addition of four-bit binary numbers. The problem will first be stated in decimal, then converted to binary, and then done. The last problem is introduced for the express purpose of pointing out an error.

We shall see in a minute that four-bit binary numbers can represent decimal numbers in the range 0 to 15 inclusive. Here are the problems, first in decimal and then in binary.

1) 6 + 1 0110 + 0001

2) 11 + 1 1011 + 0001

3) 13 + 5 1101 + 0101

0110 1011 1101 In the first sum, we add 1 to an even number. This

0001 0001 0101 is quite easy to do. Just change the last 0 to a 1.

0111 1100 0010 Otherwise, we may need to watch the carry bits.

In the second sum, let us proceed from right to left. 1 + 1 = 0 with carry = 1. The second column has 1 + 0 with carry-in of 1 = 0 with carry-out = 1. The third column has 0 + 0 with a carry-in of 1 = 1 with carry-out = 0. The fourth column is 1 + 0 = 1.

Analysis of the third sum shows that it is correct bit-wise but seems to be indicating that
13 + 5 = 2. This is an example of “busted arithmetic”, more properly called overflow. A give number of bits can represent integers only in a given range; here 13 + 5 is outside the range 0 to 15 inclusive that is proper for four-bit numbers.

Signed and Unsigned Integers

Fixed point numbers include real numbers with a fixed number of decimals, such as those commonly used to denote money amounts in the United States. We shall focus only on integers and relegate the study of real numbers to the floating point discussion.

Integers are stored in a number of formats. The most common formats today include 16 and 32 bits. The new edition of Visual Basic will include a 64–bit standard integer format.

Bits in the storage of an integer are numbered right to left, with bit 0 being the right-most or least-significant. In eight bit integers, the bits from left to right are numbered 7 to 0. In 32 bit integers, the bits from left to right are numbered 31 to 0.*

Although 32-bit integers are probably the most common, we shall focus on eight-bit integers because they are easy to illustrate. In these discussions, the student should recall the powers of 2: 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32, 2⁶ = 64, 2⁷ = 128, and 2⁸ = 256.

The simplest topic to cover is the storage of unsigned integers. As there are 2^N possible combinations of N binary bits, there are 2^N unsigned integers ranging from 0 to 2^N – 1. For eight-bit unsigned integers, this range is 0 though 255, as 2⁸ = 256. Conversion from binary to decimal is easy and follows the discussion earlier in this chapter.

Of the various methods for storing signed integers, we shall discuss only three
      Two’s complement
      One’s complement (but only as a way to compute the two’s complement)
      Excess 127 (for 8-bit numbers only) as a way to understand the floating point standard.

One’s complement arithmetic is mostly obsolete and interests us only as a stepping-stone to two’s complement arithmetic. To compute the one’s complement of a number:

1) Represent the number as an N-bit binary number
2) Convert every 0 to a 1 and every 1 to a 0.

Note that it is essential to state how many bits are to be used. Consider the 8-bit two’s complement of 100. Now 100 = 64 + 32 + 4, so decimal 100 = 0110 0100 binary. Note the leading 0; we must have an 8-bit representation. Hence, the book’s example (on page 31) of decimal 12 = 0000 1100 binary. Recall that the space in the binary is for readability only.

*NOTE:    This is not the notation used by IBM for its mainframe and enterprise computers.
                   In the IBM notation, the most significant bit (often the sign bit) is bit 0 and the
                   least significant bit has the highest number; bit 7 for an 8–bit integer.

Common Notation (8–bit entry) IBM Mainframe Notation

Bit #	7	6	5 – 1	0
	Sign	MSB		LSB

Bit #	0	1	2 – 6	7
	Sign	MSB		LSB

Decimal 100 = 0110 0100

One’s complement 1001 1011; in one’s complement, decimal –100 = 1001 1011 binary.

There are a number of problems in one’s complement arithmetic, the most noticeable being illustrated by the fact that the one’s complement of 0 is 1111 1111.

The two’s complement of a number is obtained as follows:

1) First take the one’s complement of the number

2) Add 1 to the one’s complement and discard the carry out of the left-most column.

Decimal 100 = 0110 0100

One’s complement 1001 1011

We now do the addition 1001 1011

1001 1100

Thus, in eight-bit two’s complement arithmetic

Decimal 100 = 0110 0100 binary

Decimal – 100 = 1001 1100 binary

This illustrates one pleasing feature of two’s complement arithmetic: for both positive and negative integers the last bit is zero if and only if the number is even.

The real reason for the popularity of two’s complement can be seen by calculating the representation of – 0. To do this we take the two’s complement of 0.

In eight bits, 0 is represented as 0000 0000

Its one’s complement is represented as 1111 1111.

We now take the two’s complement of 0.

Here is the addition 1111 1111
1

1 0000 0000 – but discard the leading 1.

Thus the two’s complement of 0 is represented as 0000 0000, as required by algebra, and we avoid the messy problem of having – 0 ¹ 0.

In N- bit two’s complement arithmetic,                + 127         0111 1111
the range of integers that can be                           + 10           0000 1010
represented is – 2^N-1 through 2^N-1 – 1                    +1              0000 0001
inclusive, thus the range for eight-bit                   0                0000 0000
two’s complement integers is –128                       – 1             1111 1111       The number is
through 127 inclusive, as 2⁷ = 128. The               – 10           1111 0110       negative if and
table at the right shows a number of                     – 127         1000 0001       only if the high
binary representations for this example.               – 128         1000 0000       order bit is 1.

We now give the ranges allowed for the most common two’s complement representations.
      Eight bit                – 128         to                      +127
      16-bit                – 32,768         to                 +32,767
      32-bit    – 2,147,483,648         to     +2,147,483,647

The range for 64-bit two’s complement integers is – 2⁶³ to 2⁶³ – 1. As an exercise in math, I propose to do a rough calculation of 2⁶³. This will be done using only logarithms.

There is a small collection of numbers that the serious student of computer science should memorize. Two of these numbers are the base-10 logarithms of 2 and 3. To five decimal places, log 2 = 0.30103 and log 3 = 0.47712.

Now 2⁶³ = (10^0.30103)⁶³ = 10^18.9649 = 10^0.9649 · 10¹⁸ = 9.224 · 10¹⁸, so a 64-bit integer allows the representation of 18 digit numbers and most 19 digit numbers.

Reminder: For any number of bits, in two’s complement arithmetic the number is negative if and only if the high-order bit in the binary representation is a 1.

Sign Extension

This applies to numbers represented in one’s-complement and two’s-complement form. The issue arises when we store a number in a form with more bits; for example when we store a 16-bit integer in a 32-bit register. The question is how to set the high-order bits.

Consider a 16-bit integer stored in two’s-complement form. Bit 15 is the sign bit. We can consider bit representation of the number as A₁₅A₁₄A₁₃A₁₂A₁₁A₁₀A₉A₈A₇A₆A₅A₄A₃A₂A₁A₀. Consider placing this number into a 32-bit register with bits numbered R₃₁ through R₀, with R₃₁ being the sign bit. Part of the solution is obvious: make R_k = A_k for 0 £ k £ 15. What is not obvious is how to set bits 31 through 16 in R as the 16-bit integer A has no such bits.

For non-negative numbers the solution is obvious and simple, set the extra bits to 0. This is like writing the number two hundred (200) as a five digit integer; write it 00200. But consider the 16-bit binary number 1111 1111 1000 0101, which evaluates to decimal –123. If we expanded this to 0000 0000 0000 0000 1111 1111 1000 0101 by setting the high order bits to 0’s, we would have a positive number, evaluating as 65413. This is not correct.

The answer to the problem is sign extension, which means filling the higher order bits of the bigger representation with the sign bit from the more restricted representation. In our example, we set bits 31 through 16 of the register to the sign bit of the 16-bit integer. The correct answer is then 1111 1111 1111 1111 1111 1111 1000 0101.

Note – the way I got the value 1111 1111 1000 0101 for the 16-bit representation of – 123 was to compute the 8-bit representation, which is 1000 0101. The sign bit in this representation is 1, so I extended the number to 16-bits by setting the high order bits to 1.

Nomenclature: “Two’s-Complement Representation” vs. “Taking the Two’s-Complement”

We now address an issue that seems to cause confusion to some students. There is a difference between the idea of a complement system and the process of taking the complement. Because we are interested only in the two’s-complement system, I restrict my discussion to that system.

Question: What is the representation of the positive number 123 in 8-bit two’s complement arithmetic?

Answer: 0111 1011. Note that I did not take the two’s complement of anything to get this.

Two’s-complement arithmetic is a system of representing integers in which the two’s-complement is used to compute the negative of an integer. For positive integers, the method of conversion to binary differs from unsigned integers only in the representable range.

For N-bit unsigned integers, the range of integers representable is 0 ... 2^N – 1, inclusive. For N-bit two’s-complement integers the range of non-negative integers representable is

0 ... 2^N-1 – 1, inclusive. The rules for converting decimal to binary integers are the same for non-negative integers – one only has to watch the range restrictions.

The only time when one must use the fact that the number system is two’s-complement (that is – take the two’s-complement) is when one is asked about a negative number. Strictly speaking, it is not necessary to take the two’s-complement of anything in order to represent a negative number in binary, it is only that most students find this the easiest way.

Question: What is the representation of –123 in 8-bit two’s-complement arithmetic?

Answer: Perhaps I know that the answer is 1000 0101. As a matter of fact, I can calculate this result directly without taking the two’s-complement of anything, but most students find the mechanical way the easiest way to the solution. Thus, the preferred solution for most students is

1) We note that 0 £ 123 £ 2⁷ – 1, so both the number and its negative
can be represented as an 8-bit two’s-complement integer.

2) We note that the representation of +123 in 8-bit binary is 0111 1011

3) We take the two’s-complement of this binary result to get the binary
representation of –123 as 1000 0101.

We note in passing a decidedly weird way to calculate the representations of non-negative integers in two’s-complement form. Suppose we want the two’s-complement representation of +123 as an eight-bit binary number. We could start with the fact that the representation of –123 in 8-bit two’s-complement is 1000 0101 and take the two’s complement of 1000 0101 to obtain the binary representation of 123 = –(–123). This is perfectly valid, but decidedly strange. One could work this way, but why bother?

Summary: Speaking of the two’s-complement does not mean that one must take the
two’s-complement of anything.

Excess–127

We now cover excess–127 representation. This is mentioned only because it is required when discussing the IEEE floating point standard. In general, we can consider an excess-M notation for any positive integer M. For an N-bit excess-M representation, the rules for conversion from binary to decimal are:

1) Evaluate as an unsigned binary number

2) Subtract M.

To convert from decimal to binary, the rules are

1) Add M

2) Evaluate as an unsigned binary number.

In considering excess notation, we focus on eight-bit excess-127 notation. The range of values that can be stored is based on the range that can be stored in the plain eight-bit unsigned standard: 0 through 255. Remember that in excess-127 notation, to store an integer N we first form the number N + 127. The limits on the unsigned eight-bit storage require that 0 £ (N + 127) £ 255, or – 127 £ N £ 128.

As an exercise, we note the eight-bit excess-127 representation of – 5, – 1, 0 and 4.

– 5 + 127 = 122. Decimal 122 = 0111 1010 binary, the answer.

– 1 + 127 = 126. Decimal 126 = 0111 1110 binary, the answer.

0 + 127 = 127. Decimal 127 = 0111 1111 binary, the answer.

4 + 127 = 131 Decimal 131 = 1000 0011 binary, the answer.

We have now completed the discussion of common ways to represent unsigned and signed integers in a binary computer. We now start our progress towards understanding the storage of real numbers in a computer. There are two ways to store real numbers – fixed point and floating point. We focus this discussion on floating point, specifically the IEEE standard for storing floating point numbers in a computer.

Normalized Numbers

The last topic to be discussed prior to defining the IEEE standard for floating point numbers is that of normalized numbers. We must also mention the concept of denormalized numbers, though we shall spend much less time on the latter.

A normalized number is one with a representation of the form X · 2^P, where 1.0 £ X < 2.0. At the moment, we use the term denormalized number to mean a number that cannot be so represented, although the term has a different precise meaning in the IEEE standard. First, we ask a question: “What common number cannot be represented in this form?”

The answer is zero. There is no power of 2 such that 0.0 = X · 2^P, where 1.0 £ X < 2.0. We shall return to this issue when we discuss the IEEE standard, at which time we shall give a more precise definition of the denormalized numbers, and note that they include 0.0. For the moment, we focus on obtaining the normalized representation of positive real numbers.

We start with some simple examples.

1.0 = 1.0 · 2⁰, thus X = 1.0 and P = 0.

1.5 = 1.5 · 2⁰, thus X = 1.5 and P = 0.

2.0 = 1.0 · 2¹, thus X = 1.0 and P = 1

0.25 = 1.0 · 2^-2, thus X = 1.0 and P = -2

7.0 = 1.75 · 2², thus X = 1.75 and P = 2

0.75 = 1.5 · 2^-1, thus X = 1.5 and P = -1.

To better understand this conversion, we shall do a few more examples using the more mechanical approach to conversion of decimal numbers to binary. We start with an example: 9.375 · 10^-2 = 0.09375. We now convert to binary.

0.09375 · 2 = 0.1875       0
0.1875    · 2 = 0.375         0                Thus decimal 0.09375 = 0.00011 binary
0.375      · 2 = 0.75           0                or 1.1 · 2^-4 in the normalized notation.
0.75        · 2 = 1.5             1
0.5          · 2 = 1.0             1

Please note that these representations take the form X · 2^P, where X is represented as a binary number but P is represented as a decimal number. Later, P will be converted to an excess-127 binary representation, but for the present it is easier to keep it in decimal.

We now convert the decimal number 80.09375 to binary notation. I have chosen 0.09375 as the fractional part out of laziness as we have already obtained its binary representation. We now convert the number 80 from decimal to binary. Note 80 = 64 + 16 = 2⁶ · (1 + ¼).

80 / 2 = 40 remainder 0
40/2 = 20 remainder 0

20 / 2 = 10 remainder 0

10 / 2 = 5 remainder 0

5 / 2 = 2 remainder 1

2 / 2 = 1 remainder 0

1 / 2 = 1 remainder 1

Thus decimal 80 = 1010000 binary and decimal 80.09375 = 1010000.00011 binary. To get the binary point to be after the first 1, we move it six places to the left, so the normalized form of the number is 1.01000000011 · 2⁶, as expected. For convenience, we write this as 1.0100 0000 0110 · 2⁶.

Extended Example: Avagadro’s Number.

Up to this point, we have discussed the normalized representation of positive real numbers where the conversion from decimal to binary can be done exactly for both the integer and fractional parts. We now consider conversion of very large real numbers in which it is not practical to represent the integer part, much less convert it to binary.

We now discuss a rather large floating point number: 6.023 · 10²³. This is Avagadro’s number. We shall convert this to normalized form and use the opportunity to discuss a number of issues associated with floating point numbers in general.

Avagadro’s number arises in the study of chemistry. This number relates the atomic weight of an element to the number of atoms in that many grams of the element. The atomic weight of oxygen is 16.00, as a result of which there are about 6.023 · 10²³ atoms in 16 grams of oxygen. For our discussion we use a more accurate value of 6.022142 · 10²³ obtained from the web sit of the National Institute of Standards (www.nist.gov).

We first remark that the number is determined by experiment, so it is not known exactly. We thus see one of the main scientific uses of this notation – to indicate the precision with which the number is known. The above should be read as (6.022142 ± 0.0000005) · 10²³, that is to say that the best estimate of the value is between 6.0221415 · 10²³ and 6.0221425 · 10²³, or between 602, 214, 150, 000, 000, 000, 000, 000 and 602, 214, 250, 000, 000, 000, 000, 000. Here we see another use of scientific notation – not having to write all these zeroes.

Again, we use logarithms and anti-logarithms to convert this number to a power of two. The first question is how accurately to state the logarithm. The answer comes by observing that the number we are converting is known to seven digit’s precision. Thus, the most accuracy that makes sense in the logarithm is also seven digits.

In base-10 logarithms log(6.022142 · 10²³) = 23.0 + log(6.022142). To seven digits, this last number is 0.7797510, so log(6.022142 · 10²³) = 23.7797510.

We now use the fact that log(2.0) = 0.3010300 to seven decimal places to solve the equation
2^X = (10^0.3010300)^X = 10.^23.7797520 or 0.30103·X = 23.7797510 for X = 78.9946218.

If we use N_A to denote Avagadro’s number, the first thing we have discovered from this tedious analysis is that 2⁷⁸ < N_A < 2⁷⁹, and that N_A » 2⁷⁹. The representation of the number in normal form is thus of the form 1.f · 2⁷⁸, where the next step is to determine f. To do this, we obtain the decimal representation of 2⁷⁸.

Note that 2⁷⁸ = (10^0.30103)⁷⁸ = 10^23.48034 = 10^0.48034 · 10²³ = 3.022317 · 10²³.
But 6.022142 / 3.022317 = 1.992558, so N_A = 1.992558 · 2⁷⁸, and f = 0.992558.

To complete this problem, we obtain the binary equivalent of 0.992558.

0.992558 · 2 = 1.985116        1
0.985116 · 2 = 1.970232        1
0.970232 · 2 = 1.949464        1
0.949464 · 2 = 1.880928        1
0.880928 · 2 = 1.761856        1
0.761856 · 2 = 1.523712        1
0.523712 · 2 = 1.047424        1

0.047424 · 2 = 0.094848        0
0.094848 · 2 = 0.189696        0
0.189696 · 2 = 0.379392        0
0.379392 · 2 = 0.758784        0

0.758784 · 2 = 1.517568 1

The desired form is 1.1111 1110 0001 · 2⁷⁸.

IEEE Standard 754 Floating Point Numbers

There are two primary formats in the IEEE 754 standard; single precision and double precision. We shall study the single precision format.

The single precision format is a 32-bit format. From left to right, we have
            1 sign bit; 1 for negative and 0 for non-negative
            8 exponent bits
            23 bits for the fractional part of the mantissa.

The eight-bit exponent field stores the exponent of 2 in excess-127 form, with the exception of two special bit patterns.

0000 0000 numbers with these exponents are denormalized
1111 1111 numbers with these exponents are infinity or Not A Number

Before presenting examples of the IEEE 754 standard, we shall examine the concept of NaN or Not a Number. In this discussion, we use some very imprecise terminology.

Consider the quotient 1/0. The equation 1 / 0 = X is equivalent to solving for a number X such that 0 · X = 1. There is no such number. Loosely speaking, we say 1 / 0 = ¥. Now consider the quotient 0/0. Again we are asking for the number X such that 0 · X = 0. The difference here is that this equation is true for every number X. In terms of the IEEE standard, 0 / 0 is Not a Number, or NaN.

The number NaN can also be used for arithmetic operations that have no solutions, such as taking the square root of –1 while limited to the real number system.

We now illustrate the standard by doing some conversions.

For the first example, consider the number –0.75.

To represent the number in the IEEE standard, first note that it is negative so that the sign bit is 1. Having noted this, we convert the number 0.75.

0.75 · 2 = 1.5 1

0.5 · 2 = 1.0 1

Thus, the binary equivalent of decimal 0.75 is 0.11 binary. We must now convert this into the normalized form 1.10 · 2^–1. Thus we have the key elements required.

The power of 2 is –1, stored in Excess-127 as 126 = 0111 1110 binary.

The fractional part is 10, possibly best written as 10000

Recalling that the sign bit is 1, we form the number as follows:

1 0111 1110 10000

We now group the binary bits by fours from the left until we get only 0’s.

1011 1111 0100 0000

Since trailing zeroes are not significant in fractions, this is equivalent to

1011 1111 0100 0000 0000 0000 0000 0000

or BF40 0000 in hexadecimal.

As another example, we revisit a number converted earlier. We have shown that

80.09375 = 1.0100 0000 0110 · 2⁶. This is a positive number, so the sign bit is 0. As an Excess-127 number, 6 is stored as 6 + 127 = 133 = 1000 0101 binary. The fractional part of the number is 0100 0000 0110 0000, so the IEEE representation is

0 1000 0101 0100 0000 0110 0000

Regrouping by fours from the left, we get the following

0100 0010 1010 0000 0011 0000

In hexadecimal this number is 42A030, or 42A0 3000 as an eight digit hexadecimal.

Some Examples “In Reverse”

We now consider another view on the IEEE floating point standard – the “reverse” view. We are given a 32-bit number, preferably in hexadecimal form, and asked to produce the floating-point number that this hexadecimal string represents. As always, in interpreting any string of binary characters, we must be told what standard to apply – here the IEEE-754 single precision standard.

First, convert the following 32-bit word, represented by eight hexadecimal digits, to the floating-point number being represented.

0000 0000 // Eight hexadecimal zeroes representing 32 binary zeroes

The answer is 0.0. This is a result that should be memorized.

The question in the following paragraph was taken from a CPSC 2105 mid-term exam and the paragraphs following were taken from the answer key for the exam.

Give the value of the real number (in standard decimal representation) represented by the following 32-bit words stored as an IEEE standard single precision.
            a)            4068 0000
            b)            42E8 0000
            c)            C2E8 0000
            d)            C380 0000

e) C5FC 0000

The first step in solving these problems is to convert the hexadecimal to binary.

a) 4068 0000 = 0100 0000 0110 1000 0000 0000 0000 0000
Regroup to get 0 1000 0000 1101 0000 etc.

Thus    s = 0 (not a negative number)
            p + 127 = 10000000₂ = 128₁₀, so p = 1
and                     m = 1101, so 1.m = 1.1101 and the number is 1.1101·2¹ = 11.101₂.

But 11.101₂ = 2 + 1 + 1/2 + 1/8 = 3 + 5/8 = 3.625.

b)   42E8 0000 = 0100 0010 1110 1000 0000 0000 0000 0000
Regroup to get 0 1000 0101 1101 0000 etc
Thus    s = 0 (not a negative number)
            p + 127 = 10000101₂ = 128 + 4 + 1 = 133, hence p = 6
and                     m = 1101, so 1.m = 1.1101 and the number is 1.1101·2⁶ = 1110100₂
But 1110100₂ = 64 + 32 + 16 + 4 = 96 + 20 = 116 = 116.0

c) C2E80 0000 = 1100 0010 1110 1000 0000 0000 0000 0000
Regroup to get 1 1000 0101 1101 0000 etc.
Thus s = 1 (a negative number) and the rest is the same as b). So – 116.0

d) C380 0000 = 1100 0011 1000 0000 0000 0000 0000 0000

Regroup to get 1 1000 0111 0000 0000 0000 0000 0000 000

Thus    s = 1 (a negative number)
            p + 127 = 10000111₂ = 128 + 7 = 135; hence p = 8.
            m = 0000, so 1.m = 1.0 and the number is – 1.0 · 2⁸ = – 256.0

e)   C5FC 0000 = 1100 0101 1111 1100 0000 0000 0000 0000
Regroup to get 1 1000 1011 1111 1000 0000 0000 0000 000
Thus    s = 1 (a negative number)
            p + 127 = 1000 1011₂ = 128 + 8 + 2 + 1 = 139, so p = 12
            m = 1111 1000, so 1.m = 1.1111 1000

There are three ways to get the magnitude of this number. The magnitude can be written in normalized form as 1.1111 1000 · 2¹² = 1.1111 1000 · 4096, as 2¹² = 4096.

Method 1

If we solve this the way we have, we have to place four extra zeroes after the decimal point to get the required 12, so that we can shift the decimal point right 12 places.

      1.1111 1000 · 2¹² = 1.1111 1000 0000 · 2¹² = 1 1111 1000 0000₂
                                    = 2¹² + 2¹¹+ 2¹⁰ + 2⁹ + 2⁸ + 2⁷
                                    = 4096 + 2048 + 1024 + 512 + 256 + 128 = 8064.

Method 2

We shift the decimal place only 5 places to the right (reducing the exponent by 5) to get
      1.1111 1000 · 2¹² = 1 1111 1.0 · 2⁷
                                    = (2⁵ + 2⁴ + 2³ + 2² + 2¹ + 2⁰) · 2⁷
                                    = (32 + 16 + 8 + 4 + 2 + 1) · 128 = 63 · 128 = 8064.

Method 3
This is an offbeat method, not much favored by students.

      1.1111 1000 · 2¹² = (1 + 2^–1 + 2^–2+ 2^–3+ 2^–4+ 2^–5) · 2¹²
                                    = 2¹² + 2¹¹+ 2¹⁰ + 2⁹ + 2⁸ + 2⁷
                                    = 4096 + 2048 + 1024 + 512 + 256 + 128 = 8064.

Method 4
This is another offbeat method, not much favored by students.

      1.1111 1000 · 2¹² = (1 + 2^–1 + 2^–2+ 2^–3+ 2^–4+ 2^–5) · 2¹²
                                    = (1 + 0.5 + 0.25 + 0.125 + 0.0625+ 0.03125) · 4096
                                    = 1.96875 · 4096 = 8064.

The answer is – 8064.0.

As a final example, we consider the IEEE standard representation of Avagadro’s number. We have seen that N_A = 1.1111 1110 0001 · 2⁷⁸. This is a positive number, so the sign bit is 0.

We now consider the representation of the exponent 78. Now 78 + 127 = 205, so the
Excess-127 representation of 78 is 205 = 128 + 77 = 128 + 64 + 13 = 128 + 64 + 8 + 4 + 1. As an 8-bit binary number this is 1100 1101. We already have the fractional part, so we get

0 1100 1101 1111 1110 0001 0000

Grouped by fours from the left we get

0110 0110 1111 1111 0000 1000 0000 0000

or 66FF 0800 in hexadecimal.

Range and Precision

We now consider the range and precision associated with the IEEE single precision standard using normalized numbers.. The range refers to the smallest and largest positive numbers that can be stored. Recalling that zero is not a positive number, we derive the smallest and largest representable numbers.

In the binary the smallest normalized number is 1.0 · 2^–126 and the largest number is a bit less than 2.0 · 2¹²⁷ = 2¹²⁸. Again, we use logarithms to evaluate these numbers.
– 126 · 0.30103 = – 37.93 = – 38.0 + 0.07, so 2^–126 = 1.07 · 10 ^-38, approximately.

128 · 0.30103 = 38.53, so 2¹²⁸ = 3.5 · 10 ³⁸, as 10^0.53 is a bit bigger than 3.2.

We now consider the precision associated with the standard. Consider the decimal notation 1.23. The precision associated with this is ± 0.005 as the number really represents a value between 1.225 and 1.235 respectively.

The IEEE standard has a 23-bit fraction. Thus, the precision associated with the standard is 1 part in 2²⁴ or 1 part in 16 · 2²⁰ = 16 · 1048576 = 16777216. This accuracy is more precise than 1 part in 10⁷, or seven digit precision.

Denormalized Numbers

We shall see in a bit that the range of normalized numbers is approximately 10 ^–38 to 10 ³⁸. We now consider what we might do with a problem such as the quotient 10^–20 / 10³⁰. In plain algebra, the answer is simply 10^–50, a very small positive number. But this number is smaller than allowed by the standard. We have two options for representing the quotient, either 0.0 or some strange number that clearly indicates the underflow. This is the purpose of denormalized numbers – to show that the result of an operation is positive but too small.

Why Excess–127 Notation for the Exponent?

We have introduced two methods to be used for storing signed integers – two’s-complement notation and excess–127 notation. One might well ask why two’s-complement notation is used to store signed integers while the excess–127 method is used for exponents in the floating point notation.

The answer for integer notation is simple. It is much easier to build an adder for integers stored in two’s-complement form than it is to build an adder for integers in the excess notation. In the next chapter we shall investigate a two’s-complement adder.

So, why use excess–127 notation for the exponent in the floating point representation? The answer is best given by example. Consider some of the numbers we have used as examples.

0011 1111 0100 0000 0000 0000 0000 0000 for 0.75

0100 0010 1010 0000 0011 0000 0000 0000 for 80.09375

0110 0110 1111 1111 0000 1000 0000 0000 for Avagadro’s number.

It turns out that the excess–127 notation allows the use of the integer compare unit to compare floating point numbers. Consider two floating point numbers X and Y. Pretend that they are integers and compare their bit patterns as integer bit patterns. It viewed as an integer, X is less than Y, then the floating point number X is less than the floating point Y. Note that we are not converting the numbers to integer form, just looking at the bit patterns and pretending that they are integers.

Floating Point Equality: X == Y

Due to round off error, it is sometimes not advisable to check directly for equality of floating point numbers. A better method would be to use an acceptable relative error. We borrow the notation e from calculus to stand for a small number, and use the notation |Z| for the absolute value of the number Z.

Here are two valid alternatives to the problematic statement (X == Y).

1) Absolute difference |X – Y| £ e

2) Relative difference |X – Y| £ e·(|X| +|Y|)

Note that this form of the second statement is preferable to computing the quotient
|X – Y| / (|X| +|Y|) which will be NaN (Not A Number) if X = 0.0 and Y = 0.0.

Bottom Line: In your coding with real numbers, decide what it means for two numbers to be equal. How close is close enough? There are no general rules here, only cautions. It is interesting to note that one language (SPARK, a variant of the Ada programming language does not allow floating point comparison statements such as X == Y, but demands an evaluation of the absolute value of the difference between X and Y.

Character Codes: ASCII

We now consider the methods by which computers store character data. There are three character codes of interest: ASCII, EBCDIC, and Unicode. The EBCDIC code is only used by IBM in its mainframe computer. The ASCII code is by far more popular, so we consider it first and then consider Unicode, which can be viewed as a generalization of ASCII.

The figure below shows the ASCII code. Only the first 128 characters (Codes 00 – 7F in hexadecimal) are standard. There are several interesting facts.

Last Digit \ First Digit	0	1	2	3	4	5	6	7
0	NUL	DLE	SP	0	@	P	`	p
1	SOH	DC1	!	1	A	Q	a	q
2	STX	DC2	“	2	B	R	b	r
3	ETX	DC3	#	3	C	S	c	s
4	EOT	DC4	$	4	D	T	d	t
5	ENQ	NAK	%	5	E	U	e	u
6	ACK	SYN	&	6	F	V	f	v
7	BEL	ETB	`	7	G	W	g	w
8	BS	CAN	(	8	H	X	h	x
9	HT	EM	)	9	I	Y	i	y
A	LF	SUB	*	:	J	Z	j	z
B	VT	ESC	+	;	K	[	k	{
C	FF	FS	‘	<	L	\	l	\|
D	CR	GS	-	=	M	]	m	}
E	SO	RS	.	>	N	^	n	~
F	SI	US	/	?	O	_	o	DEL

As ASCII is designed to be an 8–bit code, several manufacturers have defined extended code sets, which make use of the codes 0x80 through 0xFF (128 through 255). One of the more popular was defined by IBM. None are standard; most books ignore them. So do we.

Let X be the ASCII code for a digit. Then X – ‘0’ = X – 30 is the value of the digit.
For example ASCII(‘7’) = 37, with value 37 – 30 = 7.

Let X be an ASCII code. If ASCII(‘A’) £ X £ ASCII(‘Z’) then X is an upper case letter.
If ASCII(‘a’) £ X £ ASCII(‘z’) then X is an lower case letter.

If ASCII(‘0’) £ X £ ASCII(‘9’) then X is a decimal digit.

Let X be an upper-case letter. Then ASCII ( lower_case(X) ) = ASCII ( X ) + 32

Let X be a lower case letter. Then ASCII ( UPPER_CASE(X) ) = ASCII (X ) – 32.
The expressions are ASCII ( X ) + 20 and ASCII (X ) – 20 in hexadecimal.

Character Codes: EBCDIC

The Extended Binary Coded Decimal Interchange Code (EBCDIC) was developed by IBM in the early 1960’s for use on its System/360 family of computers. It evolved from an older character set called BCDIC, hence its name.

EBCDIC code uses eight binary bits to encode a character set; it can encode 256 characters. The codes are binary numeric values, traditionally represented as two hexadecimal digits.

Character codes 0x00 through 0x3F and 0xFF represent control characters.
            0x0D   is the code for a carriage return; this moves the cursor back to the left margin.
            0x20    is used by the ED (Edit) instruction to represent a packed digit to be printed.
            0x21    is used by the ED (Edit) instruction to force significance.
                        All digits, including leading 0’s, from this position will be printed.
            0x25    is the code for a line feed; this moves the cursor down but not horizontally.
            0x2F    is the BELL code; it causes the terminal to emit a “beep”.

Character codes 0x40 through 0x7F represent punctuation characters.
            0x40    is the code for a space character: “ ”.
            0x4B   is the code for a decimal point: “.”.
            0x4E    is the code for a plus sign: “+”.
            0x50    is the code for an ampersand: “&”.
            0x5B   is the code for a dollar sign: “$”.
            0x5C   is the code for an asterisk: “*”.
            0x60    is the code for a minus sign: “–”.
            0x6B   is the code for a comma: “,”.
            0x6F    is the code for a question mark: “?”.
            0x7C   is the code for the commercial at sign: “@”.

Character codes 0x81 through 0xA9 represent the lower case Latin alphabet.
            0x81 through 0x89      represent the letters “a” through “i”,
            0x91 through 0x99      represent the letters “j” through “r”, and
            0xA2 through 0xA9    represent the letters “s” through “z”.

Character codes 0xC1 through 0xE9 represent the upper case Latin alphabet.
            0xC1 through 0xC9    represent the letters “A” through “I”,
            0xD1 through 0xD9    represent the letters “J” through “R”, and
            0xE2 through 0xE9     represent the letters “S” through “Z”.

Character codes 0xF0 through 0xF9 represent the digits “0” through “9”.

NOTES:

1. The control characters are mostly used for network data transmissions.
The ones listed above appear frequently in user code for terminal I/O.

      2.   There are gaps in the codes for the alphabetical characters.
            This is due to the origins of the codes for the upper case alphabetic characters
            in the card codes used on the IBM–029 card punch.

3. One standard way to convert an EBCDIC digit to its numeric value
is to subtract the hexadecimal number 0xF0 from the character code.

An Abbreviated Table: The Common EBCDIC

Code	Char.	Comment	Code	Char.	Comment	Code	Char.	Comment
			80			C0	}	Right brace
			81	a		C1	A
			82	b		C2	B
			83	c		C3	C
			84	d		C4	D
			85	e		C5	E
			86	f		C6	F
			87	g		C7	G
0C	FF	Form feed	88	h		C8	H
0D	CR	Return	89	i		C9	I
16	BS	Back space	90			D0	{	Left brace
25	LF	Line Feed	91	j		D1	J
27	ESC	Escape	92	k		D2	K
2F	BEL	Bell	93	l		D3	L
40	SP	Space	94	m		D4	M
4B	.	Decimal	95	n		D5	N
4C	<		96	o		D6	O
4D	(		97	p		D7	P
4E	+		98	q		D8	Q
4F	\|	Single Bar	99	r		D9	R
50	&		A0			E0	\	Back slash
5A	!		A1	~	Tilde	E1
5B	$		A2	s		E2	S
5C	*		A3	t		E3	T
5D	)		A4	u		E4	U
5E	;		A5	v		E5	V
5F		Not	A6	w		E6	W
60	–	Minus	A7	x		E7	X
61	/	Slash	A8	y		E8	Y
6A	¦	Dbl. Bar	A9	z		E9	Z
6B	,	Comma	B0	^	Carat	F0	0
6C	%	Percent	B1			F1	1
6D	_	Underscore	B2			F2	2
6E	>		B3			F3	3
6F	?		B4			F4	4
79	‘	Apostrophe	B5			F5	5
7A	:	Colon	B6			F6	6
7B	#	Sharp	B7			F7	7
7C	@	At Sign	B8			F8	8
7D	'	Apostrophe	B9			F9	9
7E	=	Equals	BA	[	Left Bracket
7F	"	Quote	BB	]	R. Bracket

It is worth noting that IBM seriously considered adoption of ASCII as its method for internal storage of character data for the System/360. The American Standard Code for Information Interchange was approved in 1963 and supported by IBM. However the ASCII code set was not compatible with the BCDIC used on a very large installed base of support equipment, such as the IBM 026. Transition to an incompatible character set would have required any adopter of the new IBM System/360 to also purchase or lease an entirely new set of peripheral equipment; this would have been a deterrence to early adoption.

The figure below shows a standard 80–column IBM punch card produced by the IBM 029 card punch. This shows the card punch codes used to represent some EBCDIC characters.

The structure of the EBCDIC, used for internal character storage on the System/360 and later computers, was determined by the requirement for easy translation from punch card codes. The table below gives a comparison of the two coding schemes.

Character	Punch Code	EBCDIC
‘0’	0	F0
‘1’	1	F1
‘9’	9	F9
‘A’	12 – 1	C1
‘B’	12 – 2	C2
‘I’	12 – 9	C9
‘J’	11 – 1	D1
‘K’	11 – 2	D2
‘R’	11 – 9	D9
‘S’	0 – 2	E2
‘T’	0 – 8	E3
‘Z’	0 – 9	E9

Remember that the punch card codes represent the card rows punched. Each digit was represented by a punch in a single row; the row number was identical to the value of the digit being encoded.

The EBCDIC codes are eight–bit binary numbers, almost always represented as two hexadecimal digits. Some IBM documentation refers to these digits as:
The first digit is the zone potion,
The second digit is the numeric.

A comparison of the older card punch codes with the EBCDIC shows that its design was intended to facilitate the translation. For digits, the numeric punch row became the numeric part of the EBCDIC representation, and the zone part was set to hexadecimal F. For the alphabetical characters, the second numeric row would become the numeric part and the first punch row would determine the zone portion of the EBCDIC.

This matching with punched card codes explains the “gaps” found in the EBCDIC set. Remember that these codes are given as hexadecimal numbers, so that the code immediately following C9 would be CA (as hexadecimal A is decimal 10). But the code for ‘J’ is not hexadecimal CA, but hexadecimal D1. Also, note that the EBCDIC representation for the letter ‘S’ is not E1 but E2. This is a direct consequence of the design of the punch cards.

Character Codes: UNICODE

The UNICODE character set is a generalization of the ASCII character set to allow for the fact that many languages in the world do not use the Latin alphabet. The important thing to note here is that UNICODE characters consume 16 bits (two bytes) while ASCII and EBCDIC character codes are 8 bits (one byte) long. This has some implications in programming with modern languages, such as Visual Basic and Visual C++, especially in allocation of memory space to hold strings. This seems to be less of an issue in Java.

An obvious implication of the above is that, while each of ASCII and EBCDIC use two hexadecimal digits to encode a character, UNICODE uses four hexadecimal digits. In part, UNICODE was designed as a replacement for the ad–hoc “code pages” then in use. These pages allowed arbitrary 256–character sets by a complete redefinition of ASCII, but were limited to 256 characters. Some languages, such as Chinese, require many more characters.

UNICODE is downward compatible with the ASCII code set; the characters represented by the UNICODE codes 0x0000 through 0x007F are exactly those codes represented by the standard ASCII codes 0x00 through 0x7F. In other words, to convert standard ASCII to correct UNICODE, just add two leading hexadecimal 0’s and make a two–byte code.

The origins of Unicode date back to 1987 when Joe Becker from Xerox and Lee Collins and Mark Davis from Apple started investigating the practicalities of creating a universal character set. In August of the following year Joe Becker published a draft proposal for an "international/multilingual text character encoding system, tentatively called Unicode." In this document, entitled Unicode 88, he outlined a 16 bit character model:

“Unicode is intended to address the need for a workable, reliable world text encoding. Unicode could be roughly described as "wide-body ASCII" that has been stretched to 16 bits to encompass the characters of all the world's living languages. In a properly engineered design, 16 bits per character are more than sufficient for this purpose.”

In fact the 16–bit (four hexadecimal digit) code scheme has proven not to be adequate to encode every possible character set. The original code space (0x0000 – 0xFFFF) was defined as the “Basic Multilingual Plane”, or BMP. Supplementary planes have been added, so that as of September 2008 there were over 1,100,000 “code points” in UNICODE.