Design of the ALU
Adder, Logic, and the Control Unit

This lecture will finish our look at the CPU and ALU of the computer.

Remember:

1. The ALU performs the arithmetic and logic operations.

2. The control unit causes the CPU to do what the program says to do.

We begin by reviewing the binary adder, and discussing ways to speed it up.

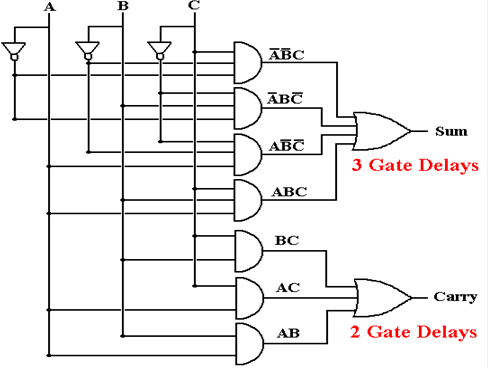
The Binary Adder

Here is a diagram of the full adder we discussed in the previous lecture.

Note the timings on the output.
After the input is valid, the carry out is valid two gate delays later.
the sum is valid three gate delays later.

Another Full Adder Implementation

Here is an implementation in Rob Williams’s book. Note the timings.

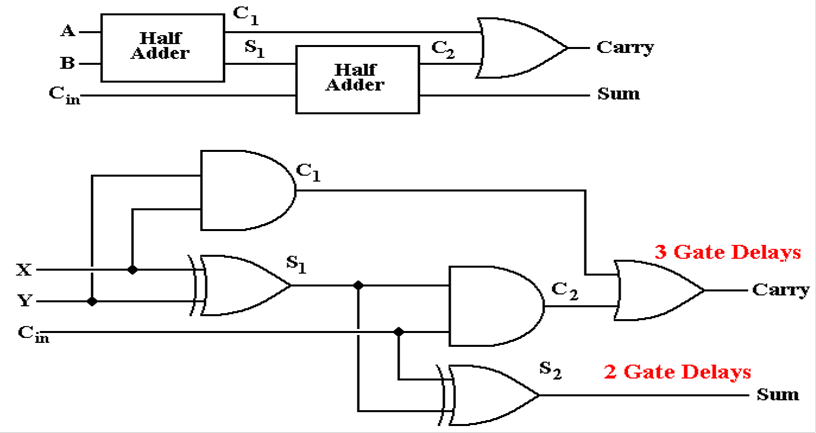
The sum is faster, but the carry–out is slower. The carry–out timing is more important.

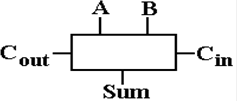
A Four–Bit Ripple–Carry Adder

Here is the symbol we often use for a full adder. It has three inputs and two outputs.

Here is a four–bit adder built from these elements. It has the timings added.

Note that the correct value of the carry “ripples” from right to left.
The sum bit is valid only after nine gate delays.

NOTE: It is the time to propagate the carry values that makes this slow.
If it were not for this problem with the carry, all values would be valid at T = 3.

For that reason, we favor designs that produce the carry bit more quickly.

The Four–Bit Adder as a Building Block

Here is a block diagram of the four–bit adder with its timings.

Here is a 16–bit adder built from four of these building blocks. Note its timings.

Consider an N–bit adder. The high order sum bit is S_N–1,
produced in 2·(N – 1) + 3 gate delays.

In general, a ripple–carry adder produces a valid N–bit sum after 2·N + 1 gate delays.

A 32–bit sum requires 65 gate delays, about 65 to 130 nanoseconds. Much too slow!

The Carry Look–Ahead Adder

Modern adders achieve greater speed by generating the carry–in to higher bits more quickly.

The standard design is a variant of the carry look–ahead adder.

Here is a taste of what that design does. In our ripple–carry adder, the carry bits are
generated independently and propagate. This takes time.

Here: C₁ = A₀·B₀ + A₀·C₀ + B₀·C₀
= A₀·B₀ + (A₀ + B₀)·C₀

Likewise: C₂ = A₁·B₁ + (A₁ + B₁)·C₁ // Wait 2 gate delays to get C₁ right.

Why not C₂ = A₁·B₁ + (A₁ + B₁)·[A₀·B₀ + (A₀ + B₀)·C₀ ]
= A₁·B₁ + (A₁ + B₁)·A₀·B₀·C₀ + (A₁ + B₁)·(A₀ + B₀)·C₀

This is messy, but it is achievable in three gate delays, not the four listed above.

The Carry Look–Ahead Adder (Part 2)

We can extend these equations to any carry bit, but let’s focus on four bits.

The notation is much simpler if we adopt standard notation: G_k = A_k · B_k
P_k = A_k + B_k

We can now write the above two equations (and the two others) as

C₁ = G₀ + P₀·C₀

C₂ = G₁ + P₁·G₀ + P₁·P₀·C₀

C₃ = G₂ + P₂·G₁ + P₂·P₁·G₀ + P₂·P₁·P₀·C₀

C₄ = G₃ + P₃·G₂ + P₃·P₂·G₁ + P₃·P₂·P₁·G₁ + P₃·P₂·P₁·P₀·C₀

This may look messy, but note the following

1. Each value of G_k and P_k can be computed independently, at the same time,
in only one gate delay.

2. Each of C₁, C₂, C₃, and C₄ can be calculated in two more gate delays,
for a total of three gate delays for each.

3. Using Rob Williams’s circuit S_k = [A_k Å B_k] Å C_k, the sum can
be computed two gate delays after the carry is valid. Each sum in 5 gate delays.

Comparison of Ripple Carry and Carry Look–Ahead

This slide shows the relative timings of the two designs for a four–bit adder.

The timings are identical for a circuit that both adds and subtracts.

The ripple–carry adder

The carry look–ahead adder.

This illustrates a classic design trick, used constantly in the development of modern
computers. Adding more hardware enables tricks to speed up the circuitry.

A More Realistic Design

Theoretically, the carry look–ahead adder can compute a 16–bit sum in 5 gate delays.

Such a design would require a few hundred basic gates. It would be hard to farbricate.

A more realistic design would be based on connecting four–bit adders.
Here is the comparison.

The ripple–carry design.

The carry look–ahead design.

This is about 2.4 times as fast as the original. Standard design tricks can be applied
to make it again twice as fast, thus five times as fast as the ripple–carry adder.

Controlling the ALU

The Control Unit (CU) is the part of the CPU that issues signals to cause the
computer to do what the program instructs it to do.

In the next few slides, we shall investigate how control signals are applied to the
Arithmetic Logic Unit (ALU).

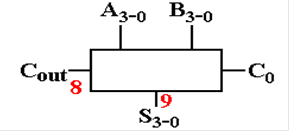
In each of the next few slides, the ALU will be considered to have two inputs (A and B)
and one output (C). The figure below uses the standard symbol for an ALU.

We begin with a very simple three–function ALU and develop the design from there.

1. C = A · B

2. C = A + B

3. C = A Å B

A real ALU must do more than this, but we just want to get an idea of its control.

Three Control Signals for Three Functions

A control signal is a binary signal with two values: asserted and not asserted.
These control signals are asserted high; TRUE (1) = Asserted and FALSE (0) = Not asserted.

A control signal is often labeled by the action it enables: here and, not, and xor.

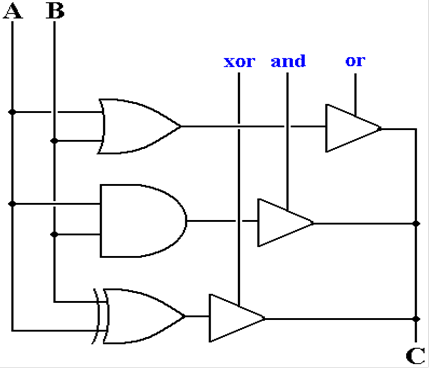
If one of these signals is asserted, the corresponding function is placed on line C.
If more than one signal is asserted, the circuit malfunctions.

Encoding the Control Signals

One way to insure that two or more control signals are not asserted at the same time is
to specify a binary code for every action.

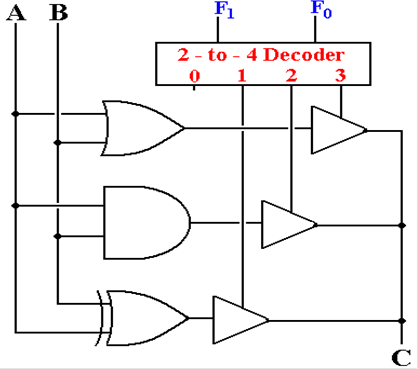
The codes are 00 Do nothing
01 Exclusive OR
10 AND
11 OR

The “Do Nothing” Option

Note that output 0 of the decoder is not attached to anything.

When the function code is 00, the ALU does not place anything on its output.
Why not specify another useful function, such as the logical NOT?

In order to see the answer, we must remember that the ALU must function in context.

Here, there are a number of devices that can put output onto the common bus.
When another device is called on to assert data on the bus, the ALU must not assert anything.

The Shift Unit

The shift unit is part of the ALU. Its function is to shift data.

There are three types of shifts:

Logical shifts

Arithmetic shifts

Circular shifts

The shift operations are very useful, though they may seem a bit strange at first.

Shift operations do not correspond to any logical operators.

Shift operations do not directly correspond to any arithmetic operators,
though the arithmetic shifts can be made to be equivalent to multiplication
and division by powers of two.

The shift operations just move bits within a register.

Double shift operations move bits within a pair of registers.

NOTE: For simplicity, we use 8–bit examples.
We assume that bit 7 is the sign bit if the 8–bit example illustrates signed integers.

Simple Logical Shifts

Here are some examples of simple logical shifts, in which a 0 is shifted into
the vacated “spot”.

The original value in binary: 1001 0110
The original value right shifted one place: 0100 1011
The original value right shifted two places 0010 0101

The original value in binary: 1001 0110
The original value left shifted one place: 0010 1100
The original value left shifted two places 0101 1000

Here are two single–bit logical shifts.

Logical Left Shift Logical Right Shift

Note that the sign bit can be changed by a logical shift

Arithmetic Shifts

Arithmetic shifts are similar to logical, except that the sign bit is preserved.

Here are two illustrations of a sequence of arithmetic shifts on positive and negative numbers.

Right Arithmetic Shift Left Arithmetic Shift

The right shift does resemble division by 2 until one gets to either 1 or –1.

The left shift occasionally resembles multiplication by 2. Note 2·104 = 208 = 128 + 80.
If the value goes outside of the range [–128, 127], shifting is not equivalent to multiplication.

Circular Shifts

Here the bits are wrapped around; nothing is lost.

In this example, a left circular shift by N bits is the same as a right circular shift by (8 – N).

For 32 bits, the equivalence is N and (32 – N).

Double Shifts

Here is an arithmetic right double shift as might be implemented on the IBM Mainframe.

In this architecture

1. Integer registers are numbered 0 through 15, and identified by number.

2. Double register shifts are applied to even–odd pairs, such as (8, 9) or (10, 11).
If the pair below were (4, 5), the instruction might be SRDA 4, 1.

Most architectures support six types of double shifts: three double left shifts
and three double right shifts.

Each of left and right can be logical, arithmetic, or circular.

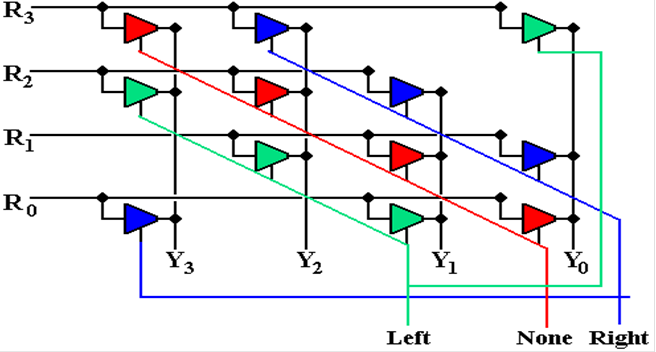
A Four–Bit Circular Barrel Shifter

A barrel shifter can do all of the shifting in one step.

An N–bit barrel shifter is implemented with N² tri–state buffers.
For this reason, it is hard to draw large barrel shifters.

Here is the example, with 3 options: no shift, circular left by 1, and circular right by 1.