Binary Adders: Half Adders and Full Adders

In this set of slides, we present the two basic types of adders:

1. Half adders, and

2. Full adders.

Each type of adder functions to add two binary bits.

In order to understand the functioning of either of these circuits, we
must speak of arithmetic in terms that I learned in the second grade.

In the first grade, I learned by “plus tables”, specifically the sum of adding
any two one–digit numbers: 2 + 2 = 4, 2 + 3 = 5, etc.

In the second grade, I learned how to add numbers that had more than one
digit each: 23 + 34 = 57, but 23 + 38 = 61.

This adaptation of addition to multiple digit numbers gives rise to the full adder.

Some Sample Sums, with Comments

We begin with two simple sums, each involving only single digits.

2 + 2 = 4, and 5 + 5 = 10.

If these are so, why do we write the following sum 25 + 25 as

25 + 25 = 50, and not as

25 + 25 = 4 10? What digit is written in the unit’s column of the sum?

The reason that we do not do this is the idea of a carry from the unit’s
column to the ten’s column.

In the language of the second grade, we describe the addition as follows:

1. 5 + 5 is 0, with a carry–out of 1, which goes into the ten’s column.

2. 2 + 2 is 4, but we have a carry–in of 1 from the unit’s column,
so we say 2 + 2 + 1 = 5. The sum digit in this column is a 5.

Positional Notation in Arithmetic

In standard decimal arithmetic, the number 25 is read as “twenty five”, and
represents 2 · 10 + 5 · 1: two tens plus five ones.

Remember that the only digits used in binary numbers are 0 and 1.

In binary arithmetic, the number 10 is read as “one zero”, avoiding the
names we use for decimal numbers. It represents 1 · 2 + 0 · 1.

In binary arithmetic, the number 101 represents 1·2² + 0·2¹ + 1·1, or
1·4 + 0·2 + 1·1 = 4 + 1 = 5.

In all arithmetics: 0 + 0 = 0,
0 + 1 = 1, and
1 + 0 = 1.

In decimal arithmetic: 1 + 1 = 2.

In binary arithmetic what is 1 + 1?
The Sum 1 + 1 in Binary Arithmetic

We have just noted that the decimal number 2 is represented in binary as 10.

It must be the case that, in binary addition, we have the sum as

1 + 1 = 10

This reads as “the addition 1 + 1 results in a sum of 0 and a carry–out of 1”.

Recall the decimal sum 25 + 25.

1
2 5
2 5
5 0

The 1 written above the numbers in the ten’s column shows the carry–out
from the unit’s column as a carry–in to the ten’s column.

The Half Adder

The half adder takes two single bit binary numbers and produces
a sum and a carry–out, called “carry”.

Here is the truth table description of a half adder. We denote the sum A + B.

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Written as a standard sum, the last row represents the following:

01
+ 01
10

The sum column indicates the number to be written in the unit’s column,
immediately below the two 1’s. We write a 0 and carry a 1.
The Half Adder and the Full Adder

In all versions of arithmetic, including binary and decimal, the half adder
represents what we do for the unit’s column when we add integers.

There is no possibility of a carry–in for the unit’s column, so we do not design
for such. Another way is to say that there is a carry–in; it is always 0.

The full adder in decimal arithmetic would be used for the other columns:
the ten’s column, the hundred’s column, and so on.

For these columns, a non–zero carry–in is a distinct possibility

Considered this way, we might write our sums table as follows.
2 + 2 = 4, if the carry–in is 0, and
2 + 2 = 5, when the carry–in is 1.

Admittedly, the complexities of decimal arithmetic suggest another way,
just add the values as three numbers, here 2 + 2 + 1 = 5.

Implementing the Half Adder

Here again is the truth table for the half adder.

A	B	Sum	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

We need equations for each of the Sum and Carry. Because we have used a
truth table to specify these functions, we consider Boolean expressions.

Note that the carry is the logical AND of the two inputs: Carry = A·B.

The sum can be given in two equivalent expressions.
The simplest expression uses the exclusive OR function: Sum = AÅB.
An equivalent expression in terms of the basic AND, OR, and NOT is:

Circuits for the Half Adder

Here are two slightly different circuit implementations of the half adder.

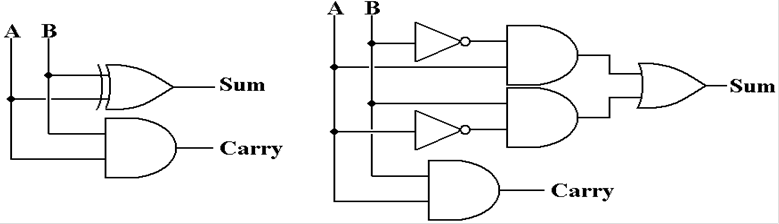
The circuit on the left implements the sum function as Sum = AÅB.

The circuit on the right implements the sum function as

Implementing the Full Adder

Here we show the truth table for the sum of A and B, with carry–in of C.

A	B	C	Sum	Carry
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

To read this as decimal, pretend that the Sum is “Sum_Bit” and read as
the Decimal_Sum = Carry·2 + Sum_Bit.

So 1 + 1 + 0 = 1·2 + 0 = 2 (decimal), and
1 + 1 + 1 = 1·2 + 1 = 3 (decimal).

One Circuit for the Full Adder

Here is the traditional AND/OR implementation of the full adder.

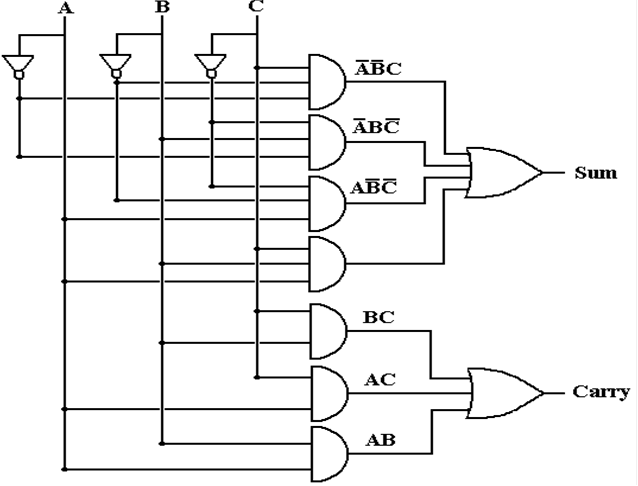
Another Circuit for the Full Adder

The slide above gave the standard design of a full adder with a grouping of
AND gates followed by an OR gate. Here is another implementation of the
SUM function using exclusive OR.

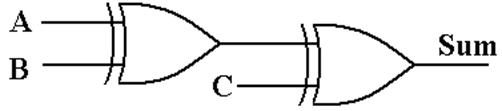
A	B	C	(A Å B)	(A Å B) Å C
0	0	0	0	0
0	0	1	0	1
0	1	0	1	1
0	1	1	1	0
1	0	0	1	1
1	0	1	1	0
1	1	0	0	0
1	1	1	0	1

The Full Adder with C = 0

The circuit above implements the following two expressions, where C is
the carry–in to the full adder.

Sum = ··C + ·B· + A·· + A·B·C

Carry = A·B + A·C + B·C

Suppose we let the carry–in C = 0. Then = 1.
What we have then is as follows.

Sum = ··0 + ·B·1 + A··1 + A·B·0
= ·B + A·

Carry = A·B + A·0 + B·0
= A·B

As expected, a full adder with carry–in set to zero acts like a half adder.

The Full–Adder and Half–Adder as Circuit Elements

When we build circuits with full adders or half adders, it is important to focus
on the functionality and not on the implementation details.

For this reason, we denote each circuit as a simple box with inputs and outputs.

The figure on the left depicts a full–adder with carry–in as an input.

The figure on the right depicts a half–adder with no carry–in as input.

The figure in the middle depicts a full–adder acting as a half–adder.

A Four–Bit Full–Adder

Here is a depiction of a four–bit full adder to add two binary numbers,
depicted as A₃A₂A₁A₀ and B₃B₂B₁B₀.

Note that the carry–out from the unit’s stage is carried into the two’s stage.
In general, the carry is propagated from right to left, in the same manner as
we see in manual decimal addition. This is called a “ripple carry adder”.

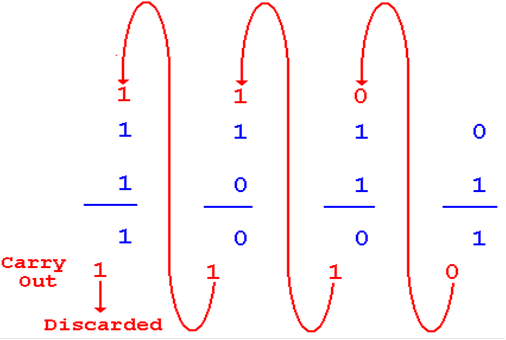
Here is an example of its output. The 4–bit sum is truncated to 1001.

1110
+ 1011
11001

Note that the unit’s adder is implemented using a full adder.

Propagating the Carry Bits

Just as in standard arithmetic, when done by hand, the carry of one stage
is propagated as a carry–in to the next higher stage.

Addition and Subtraction

In order to convert a ripple–carry adder into a subtractor, we employ
the standard algebra trick: A – B is the same as A + (–B).

In order to subtract B from A, it is necessary to negate B to produce
–B, and then to add that number to A.

We now have to develop a circuit that will negate a binary value.

In order to do this, we must stipulate the method used to represent
signed integers. As in earlier lecture, we use two’s–complement notation.

In this method, in order to negate a binary integer, it is necessary to
produce the two’s–complement of that value.

1. First, take the one’s–complement of the binary integer, and then
2. Add 1 to that value.

We have to develop a circuit to create the one’s–complement of a binary
integer. We shall develop two circuits to do this.

The One’s Complement of a Binary Integer

In order to take the one’s–complement of an integer in binary form, just
change every 0 to a 1, and every 1 to a 0. Here are some examples.

Original value 0110 0111 1010 0011
One’s complement 1001 1000 0101 1100

The circuit that does this conversion is the NOT gate. The circuit below
would be used for four–bit integers.

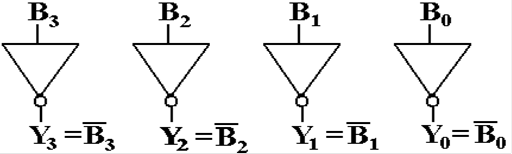
If the input is B₃B₂B₁B₀ = 0110, the output is Y₃Y₂Y₁Y₀ = 1001.

This circuit can be extended to any number of bits required.

The XOR Gate as a NOT Gate

In order to make an adder/subtractor, it is necessary to use a gate that can
either pass the value through or generate its one’s–complement.

The exclusive OR gate, XOR, is exactly what we need.

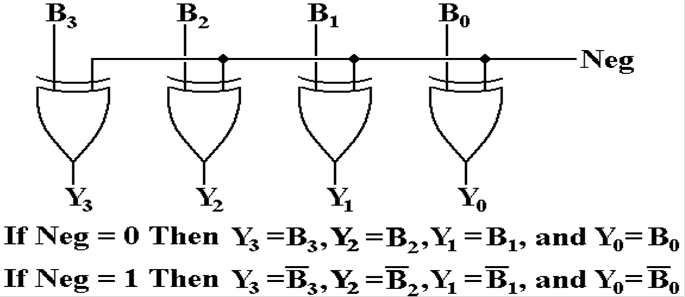
This is controlled by a single binary signal: Neg.

Let B = 1011. If Neg = 0, then Y = 1011. If Neg = 1, then Y = 0100.

Some Notation for Bit–Wise Operations

Taking the one’s–complement of a binary integer involves taking the
one’s–complement of each of its bits. We use the NOT notation to
denote the one’s–complement of the entire integer.

If B = B₃B₂B₁B₀ is a four–bit binary number, its one’s–complement is
.

Remember that to get the two’s–complement, one takes the one’s–complement
and adds one. In two’s–complement arithmetic we have: .

This suggests the use of an adder to produce the negative. For B = B₃B₂B₁B₀,
we take the one’s complement to start the negation process. The addition of 1,
necessary to take the two’s–complement, is achieved by setting the carry–in of the unit’s full–adder to 1.

This is the reason for using a full–adder in the unit’s position. We can alternate
between an adder and subtractor. More on this a bit later.

The Negator Circuit

Here is the circuit to produce the negative of a 4–bit number B = B₃B₂B₁B₀.

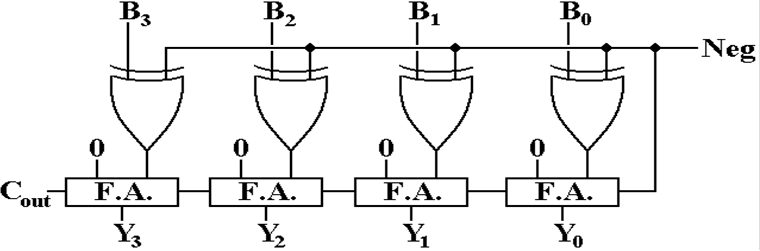
If Neg = 0, then the XOR gates pass the values B₃B₂B₁B₀ unchanged and
the ripple–carry adder adds 0 to that. The result is Y = B.

If Neg = 1, then the XOR gates cause the one’s–complement of B = B₃B₂B₁B₀
to be computed. Note that the carry–in of the full adder is set to 1, so that it
adds 1 to the one’s–complement, thus producing the negative: Y = – B.

The Full Adder/Subtractor

We now have the circuit that either adds or subtracts. This is a 4–bit circuit
that produces either (A + B) or (A – B).

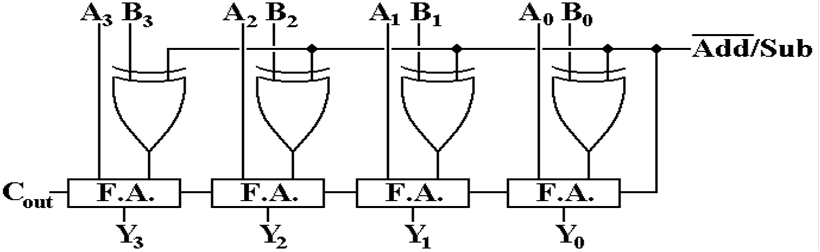
This notation is used for a two–valued control signal. When the value is 0, the
circuit is to add, when it is 1 the circuit is to subtract.

This adder/subtractor can be extended to any number of binary bits.

Overflow: “Busting the Arithmetic”

The range of 16–bit two’s–complement arithmetic is

– 32,768 to 32,767

Consider the following addition problem: 24576 + 24576.
Now + 24,576 (binary 0110 0000 0000 0000) is well within the range.

0110 0000 0000 0000 24576
0110 0000 0000 0000 24576
1100 0000 0000 0000 – 16384

What happened?

We had a carry into the sign bit. This is “overflow”. The binary representation
being used cannot handle the result.

NOTE: This works as unsigned arithmetic.
24,576 + 24,576 = 49,152 = 32768 + 16384.

Detecting Overflow

For addition, overflow occurs in only two situations:
1) Two positive integers are added and the result is negative.
2) Two negative integers are added and the result is positive.

Consider the 16–bit examples shown above. Remember that the bits are numbered
left to right as 15 down to 0, with bit 15 being the sign bit for signed representations.

Look at the full adder responsible for adding the sign bit for two integers: A and B.

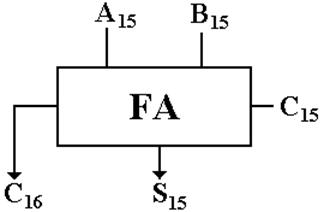
The overflow condition is now: A₁₅ == 0, B₁₅ == 0, and S₁₅ ==1, or
A₁₅ == 1, B₁₅ == 1, and S₁₅ ==0.

Implementing the Detector

Here we show the truth table for the sign bit.

A15	B15	C15	S15	C16
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Rows 1 and 6 are the only two rows in which overflow occurs. These two
rows share one interesting property: C₁₅ ¹ C₁₆, or C₁₅ Å C₁₆ = 1.

The use of this property allows overflow to be detected efficiently.

Gate Delays

Consider three gates, each of which has input that has not changed for
some time. The output of each gate correctly implements its Boolean function.

We now consider what happens as the input to each gate is changed
suddenly. Note that the output does not change at the same time as the input.

For a short time, called a “hazard”, the output of the gate is not that
of the Boolean function supposedly implemented.

Gate Delays (More)

For the time duration of one gate delay, the outputs do not match the inputs.

After one gate delay (about 2 to 10 nanoseconds) the output is correct.

Full Adder with Gate Delays (Before Input Changes)

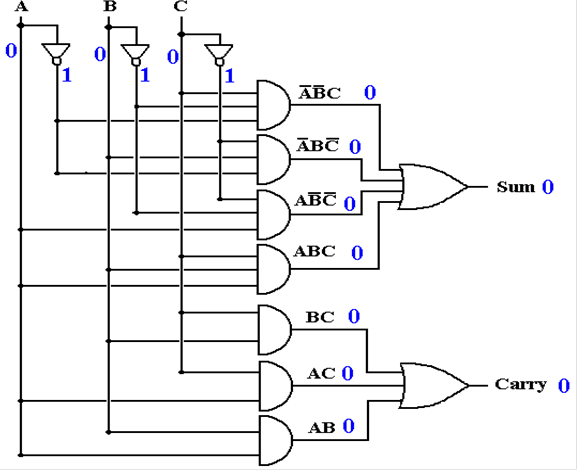
Assume the inputs have been stable for some time.

Full Adder with Gate Delays (Input Changes at T = 0)

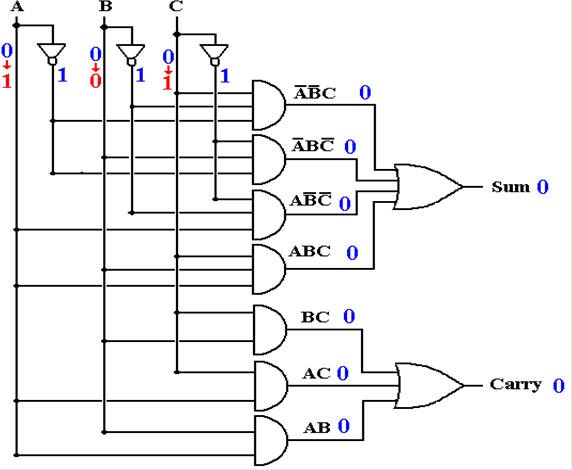
At this point, no outputs are correct.

Full Adder with Gate Delays (T = 1)

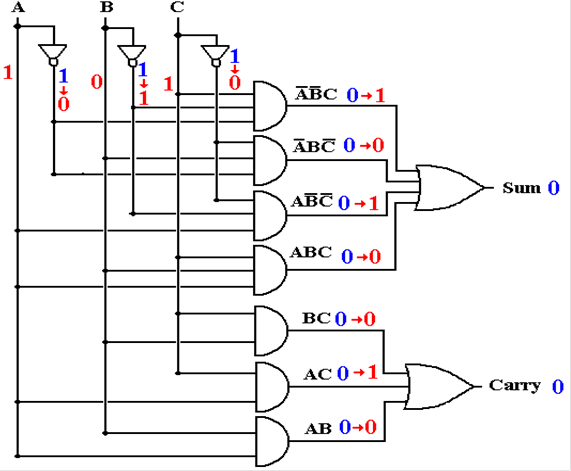
Some output is correct, but the upper AND gates are reacting to input at T = 0.

Full Adder with Gate Delays (T = 2)

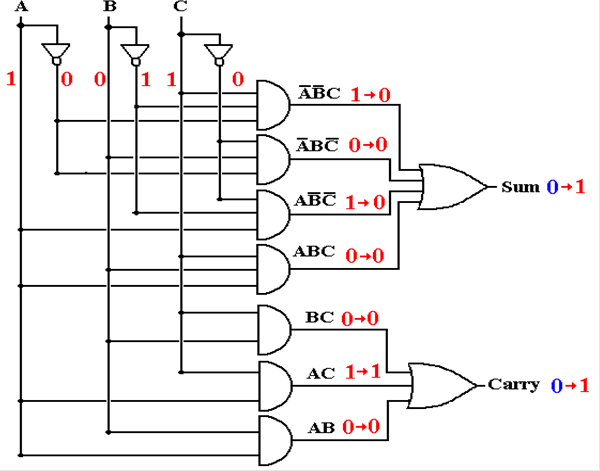
The carry out is correct, but the sum out is reacting to input at T = 1.

Full Adder with Gate Delays (T = 3)

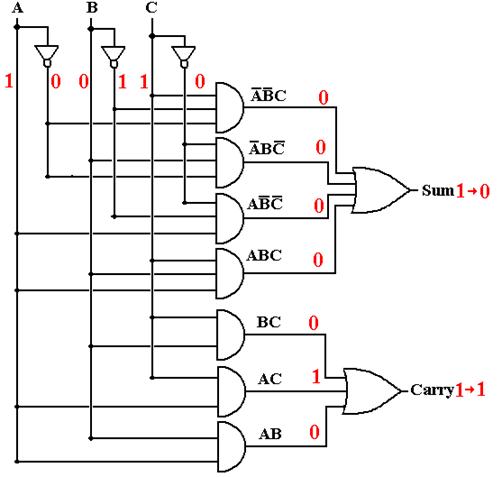
At T = 3 (and later), all output is correct.

The Ripple–Carry Adder

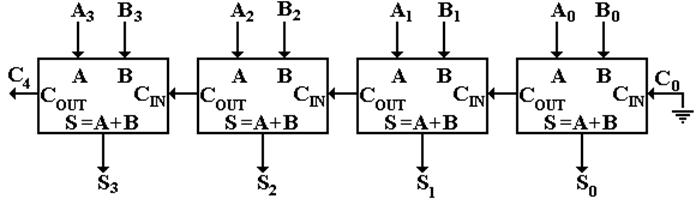
Carry–in to stage K (bit K) is valid at T = 2·K.

Carry–out from stage K is valid at T = 2·K + 2.

Sum from stage K is valid at T = 2·K + 3.

32–bit sum valid after stage 31 finishes (65 gate delays)
This circuit is not used in commercial computers.