Other Small Scale Integration Circuits

In this lecture, we discuss two of the more common SSI (Small Scale
Integrated) circuits: the Decoder and the Multiplexer.

These are combinational circuits built from the basic logic gates, which are
AND, OR, NOT, and XOR.

These SSI chips allow us to specify our design at a higher level, thus
focusing on the function of a circuit and not its basic implementation.

The building blocks that we discuss today are as follows:

The decoder, which can be viewed as producing the unsigned decimal
equivalent of a binary code with a fixed number of bits.

The multiplexer, which selects one of a number of inputs and passes it
to the output.

The tuner on a standard TV functions as a multiplexer, selecting one of the
incoming number of channels and passing it to the display circuitry.

Review of Binary Codes

These devices are based on binary coded input. We review simple binary codes
that would be used on smaller decoders and multiplexers.

2–bit codes: 00 0 3–bit codes: 000 0
01 1 001 1
10 2 010 2
11 3 011 3
100 4
101 5
110 6
111 7

The 4–bit codes are simply the unsigned binary representation of 0 – 15.
0000 is 0, 0001 is 1, 0010 is 2, 0011 is 3,
0100 is 4, 0101 is 5, 0110 is 6, 0111 is 7,
1000 is 8, 1001 is 9, 1010 is 10, 1011 is 11,
1100 is 12, 1101 is 13, 1110 is 14, 1111 is 15.

Decoders

Decoders are the opposite of encoders; they are N–to–2^N devices.

Typical examples include 2–to–4 decoders

3–to–8 decoders

4–to–16 decoders

Due to the prevalence of decimal arithmetic, we also have 4–to–10 decoders.

These are specialized 4–to–16 decoders with six fewer pins.

N–to–2^N decoders have N inputs, labeled X₀, X₁, …., X_N–1

2^N outputs, similarly labeled Y₀, Y₁, etc.

optionally, an enable line.

Decoders come in two varieties: active high and active low.

We focus our lectures on active high decoders:
the selected output goes to logic 1
the outputs not selected stay at logic 0.

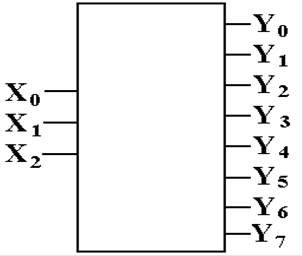
A 3–to–8 Decoder (Simple View)

Here is the symbol that might be used to represent a 3–to–8 decoder.
It is a bit simplistic in that it leaves out several important features.

The binary input selects the one output that is to be active. All other
outputs are inactive.

If X₂ = 1, X₁ = 0, X₀ = 1, then Y₅ is the
selected output to be active. All other
outputs are not active.

In a similar fashion, each of the 8 possible
binary codes activates exactly one of the
outputs, with all others not active.

Small decoders (2–to–4, 3–to–8, and 4–to–16) are often used in
digital design work.

Description of a 3–to–8 Decoder

This decoder has three inputs: X₂, X₁, X₀
eight outputs: Y₀, Y₁, Y₂, Y₃, Y₄, Y₅, Y₆, Y₇

Its functioning is best described by a modified truth table.

X2	X1	X0	Action
0	0	0	Y0 = 1, all others are 0
0	0	1	Y1 = 1, all others are 0
0	1	0	Y2 = 1, all others are 0
0	1	1	Y3 = 1, all others are 0
1	0	0	Y4 = 1, all others are 0
1	0	1	Y5 = 1, all others are 0
1	1	0	Y6 = 1, all others are 0
1	1	1	Y7 = 1, all others are 0

This gives rise to the equations:

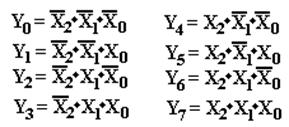
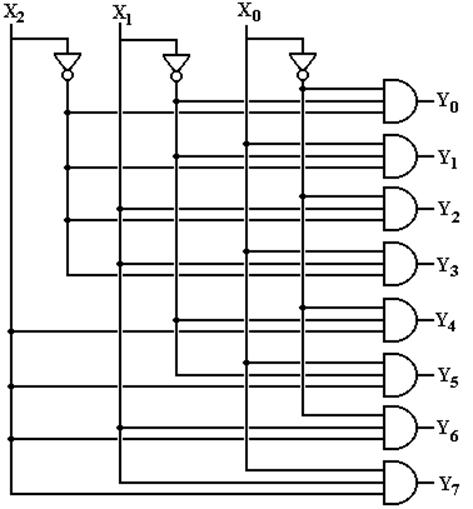
Circuit for a 3–to–8 Decoder

This follows from the equations.

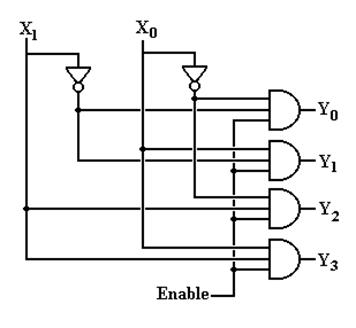
The Enable Input

Again, in the above circuit one output will always be active.

Suppose we want to have a decoder with no outputs active.

This is the function of the enable input, often denoted as “E”.

In an enabled high decoder, when E = 0 no output is active

when E = 1 the selected output is active

Here is the circuit diagram for a 2–to–4 decoder with enable input.

Multiplexers and Demultiplexers

Multiplexer – MUX
Associates One of Many Inputs to a Single Output

Demultiplexer – DEMUX
Associates One Input with One of Many Outputs

Circuit Inputs Control Outputs
Signals

Multiplexer 2^N N 1
Demultiplexer 1 N 2^N

Sample: 4–to–1 MUX and 1–to–4 DEMUX

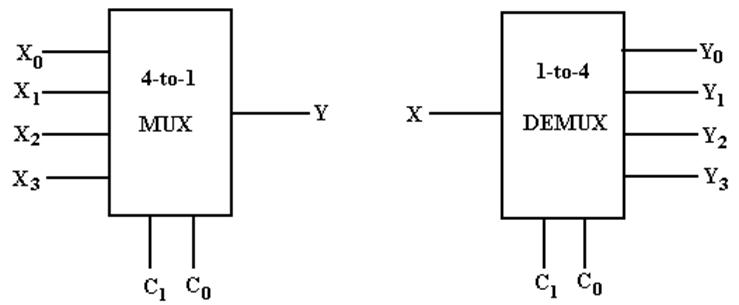
My Notation: X for Input
C for Control Signals
Y for Output

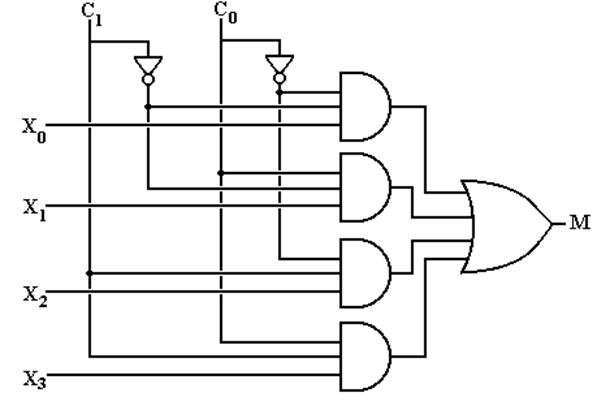
The Multiplexer Equation
Illustrated for a 4–to–1 MUX

Truth table Denote the multiplexer output by M

C1	C0	M
0	0	X0
0	1	X1
1	0	X2
1	1	X3

Equation Form

Here is another form of the equation that is better when X is used as an input.

Build a 4–to–1 MUX

But what about an enable input for a multiplexer?

What does it mean for the output of the MUX to be 0?

Build a 1–to–4 DEMUX
With an Enable

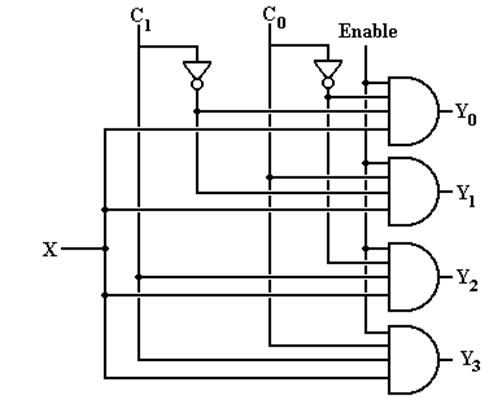
If Enable = 0, all outputs are 0.